प्राइम का एल्गोरिथम

इस ट्यूटोरियल में, आप जानेंगे कि प्राइम का एल्गोरिथम कैसे काम करता है। इसके अलावा, आप C, C ++, जावा और पायथन में प्राइम के एल्गोरिथम के काम करने के उदाहरण पाएंगे।

प्राइम का एल्गोरिथ्म एक न्यूनतम फैले हुए पेड़ का एल्गोरिथ्म है जो एक ग्राफ को इनपुट के रूप में लेता है और उस ग्राफ के किनारों का सबसेट ढूंढता है

एक पेड़ बनाएं जिसमें हर शिखर शामिल हो
उन सभी पेड़ों के बीच न्यूनतम वजन होता है जो ग्राफ से बन सकते हैं

प्राइम का एल्गोरिदम कैसे काम करता है

यह लालची एल्गोरिदम नामक एल्गोरिदम के एक वर्ग के अंतर्गत आता है जो वैश्विक इष्टतम खोजने की उम्मीद में स्थानीय इष्टतम को ढूंढता है।

हम एक शीर्ष से शुरू करते हैं और अपने लक्ष्य तक पहुंचने तक सबसे कम वजन के साथ किनारों को जोड़ते रहते हैं।

प्राइम के एल्गोरिदम को लागू करने के चरण निम्नानुसार हैं:

यादृच्छिक पर चुने गए एक शीर्ष के साथ न्यूनतम फैले हुए पेड़ की शुरुआत करें।
सभी किनारों को खोजें जो पेड़ को नए सिरे से जोड़ते हैं, न्यूनतम खोजें और इसे पेड़ में जोड़ें
चरण 2 को तब तक दोहराते रहें जब तक कि हमें न्यूनतम फैले हुए वृक्ष न मिलें

प्राइम के एल्गोरिथ्म का उदाहरण

एक भारित ग्राफ से शुरू करें

एक शीर्ष

चुनें इस शीर्ष से सबसे छोटी धार चुनें और इसे जोड़ें

निकटतम समाधान में अभी तक नहीं

चुनें। निकटतम किनारे को चुनें समाधान में अभी तक नहीं, यदि कई विकल्प हैं, तो यादृच्छिक पर एक चुनें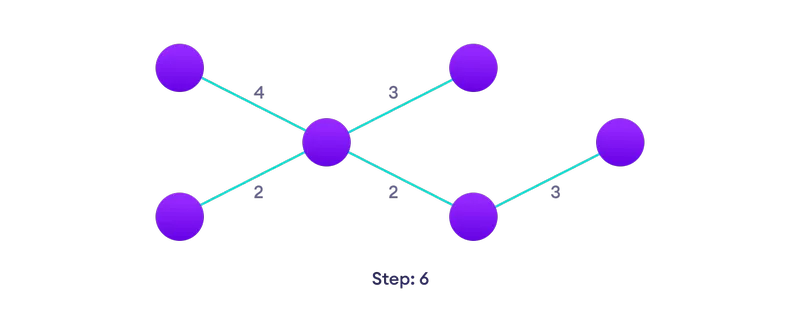

जब तक आप दोहराएं एक फैले हुए पेड़ है

प्राइम का एलगोरिदम स्यूडोकोड

प्राइम के एल्गोरिथ्म के लिए छद्मकोड दिखाता है कि हम दो सेट U और VU कैसे बनाते हैं। U में उन शीर्ष रेखाओं की सूची है, जिन्हें विज़िट किया गया है और VU ऐसे शीर्षकों की सूची है जो नहीं किए गए हैं। एक के बाद एक, हम कम से कम वज़न के किनारे को जोड़कर सेट VU से यू को स्थानांतरित करते हैं।

 T = ∅; U = ( 1 ); while (U ≠ V) let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U; T = T ∪ ((u, v)) U = U ∪ (v)

पायथन, जावा और सी / सी ++ उदाहरण

यद्यपि रेखांकन के आसन्न मैट्रिक्स प्रतिनिधित्व का उपयोग किया जाता है, इस एल्गोरिथ्म को इसकी दक्षता में सुधार करने के लिए निकटता सूची का उपयोग करके भी लागू किया जा सकता है।

पायथन जावा सी सी ++

 # Prim's Algorithm in Python INF = 9999999 # number of vertices in graph V = 5 # create a 2d array of size 5x5 # for adjacency matrix to represent graph G = ((0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)) # create a array to track selected vertex # selected will become true otherwise false selected = (0, 0, 0, 0, 0) # set number of edge to 0 no_edge = 0 # the number of egde in minimum spanning tree will be # always less than(V - 1), where V is number of vertices in # graph # choose 0th vertex and make it true selected(0) = True # print for edge and weight print("Edge : Weight") while (no_edge  G(i)(j): minimum = G(i)(j) x = i y = j print(str(x) + "-" + str(y) + ":" + str(G(x)(y))) selected(y) = True no_edge += 1

 // Prim's Algorithm in Java import java.util.Arrays; class PGraph ( public void Prim(int G()(), int V) ( int INF = 9999999; int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false boolean() selected = new boolean(V); // set selected false initially Arrays.fill(selected, false); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in // graph // choose 0th vertex and make it true selected(0) = true; // print for edge and weight System.out.println("Edge : Weight"); while (no_edge < V - 1) ( // For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise // choose another vertex nearest to selected vertex at step 1. int min = INF; int x = 0; // row number int y = 0; // col number for (int i = 0; i < V; i++) ( if (selected(i) == true) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) System.out.println(x + " - " + y + " : " + G(x)(y)); selected(y) = true; no_edge++; ) ) public static void main(String() args) ( PGraph g = new PGraph(); // number of vertices in grapj int V = 5; // create a 2d array of size 5x5 // for adjacency matrix to represent graph int()() G = ( ( 0, 9, 75, 0, 0 ), ( 9, 0, 95, 19, 42 ), ( 75, 95, 0, 51, 66 ), ( 0, 19, 51, 0, 31 ), ( 0, 42, 66, 31, 0 ) ); g.Prim(G, V); ) )

 // Prim's Algorithm in C #include #include #define INF 9999999 // number of vertices in graph #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight printf("Edge : Weight"); while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) printf("%d - %d : %d", x, y, G(x)(y)); selected(y) = true; no_edge++; ) return 0; )

 // Prim's Algorithm in C++ #include #include using namespace std; #define INF 9999999 // number of vertices in grapj #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight cout << "Edge" << " : " << "Weight"; cout << endl; while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) cout << x << " - " << y << " : " << G(x)(y); cout << endl; selected(y) = true; no_edge++; ) return 0; )

प्राइम्स बनाम क्रुस्लक का एल्गोरिदम

क्रुस्कल का एल्गोरिथ्म एक अन्य लोकप्रिय न्यूनतम फैले हुए पेड़ का एल्गोरिथ्म है जो एक ग्राफ़ के एमएसटी को खोजने के लिए एक अलग तर्क का उपयोग करता है। एक शीर्ष से शुरू करने के बजाय, क्रुस्कल का एल्गोरिथ्म कम वजन से उच्च तक सभी किनारों को सॉर्ट करता है और सबसे कम किनारों को जोड़ता रहता है, उन किनारों को अनदेखा करता है जो एक चक्र बनाते हैं।